输入装配阶段

三维模型本质是成千上万的顶点数据，比如一个正方形就有8个顶点，输入装配阶段则是对于模型顶点的第一次处理，将顶点装配成图元

该阶段不可编程

顶点着色阶段

顶点着色器会遍历传入的每一个顶点进行着色，注意，虽然叫着色器，但并不是字面意义上“计算颜色”，顶点着色阶段还有很多额外的操作，比如最重要的操作就是空间转换

模型空间

所谓模型空间，就是3D建模软件中的空间

世界空间

世界空间，是模型导入U3D之后的空间，模型在模型空间和世界空间中会一样吗？那显然未必，因为我们可以在U3D中对导入的模型进行缩放旋转位移等操作

我们称缩放矩阵为S，旋转矩阵为R，平移矩阵为T，注意顺序只能是：缩放->旋转->平移

即如果有一个模型空间中的点A，想要转换到世界空间B，则B=(TRS)*A

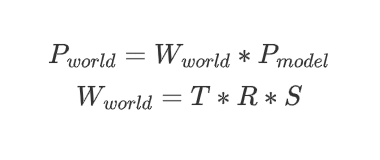
image-20211015003204195

观察空间

所谓观察空间，是从摄像机是角度出发看到的空间，Scene视图是世界空间，Game视图就是摄像机空间

根据上一篇内容可以知道，我们只要能够得到观察空间的3个基底向量在世界空间中的表示，就可以得到对应的变换矩阵了

首先我们定义一下我们的观察空间

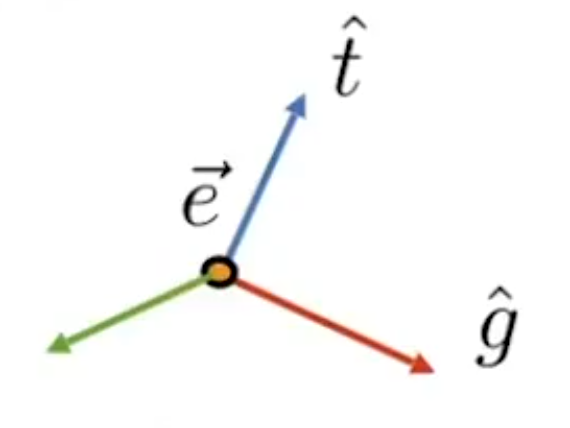
image-20211014232434401

定义摄像机原地为e，上方向为t，看着的方向为g，那么自然可以得到右方向为gxt

我们是想要从世界空间变换到观察空间

但很有意思的是， 摄像机他本身也是在世界空间中啊

所以我们可以假设有一个理想状态，相机原点就是世界原点，t轴指向Y，g轴指向Z，那么gxt自然就指向X

此时观察空间就等于世界空间！

那么问题就变成了，如何将现在的摄像机转化成一个理想状态下的摄像机？

首先平移矩阵是很好写的，因为知道摄像机的原点坐标e，那么想把摄像机平移到原点，矩阵自然为：

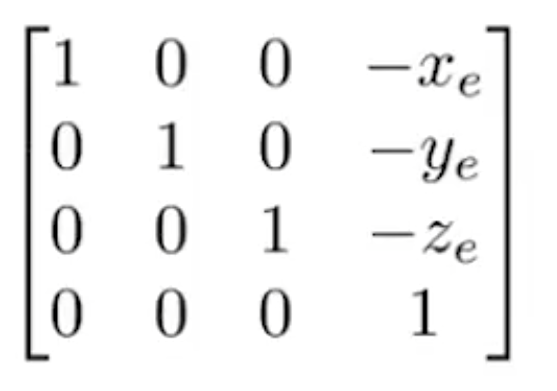
image-20211014234811382

而且这里也不存在缩放矩阵，那么自然是只剩下一个旋转矩阵了，即，通过某一个旋转矩阵，把摄像机的3个轴旋转至和世界坐标轴重合

这是比较困难的

但是，世界坐标轴我们是知道的，即（1,0,0）（0,1,0）（0,0,1），反过来想，将这3个的轴旋转到摄像机轴，应该很简单吧？

确实如此，我们能直接给出旋转矩阵：

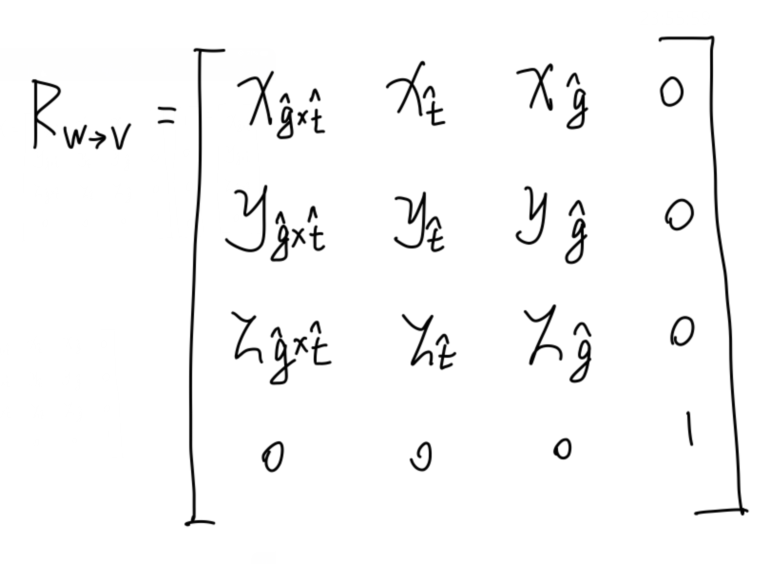
image-20211014235613415

不难验证

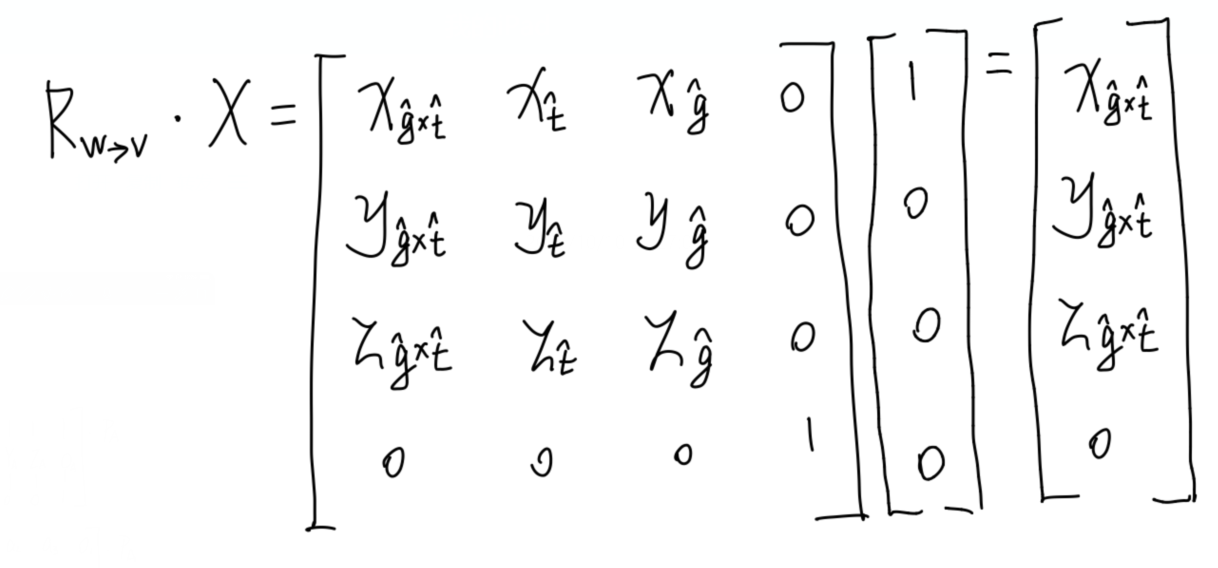
image-20211014235645901

说明这个矩阵确实能把世界空间的3个轴旋转至观察空间

那么反过来，观察空间至世界空间的旋转矩阵就是这个矩阵的逆矩阵了，而且旋转矩阵是一个正交矩阵，所以有：

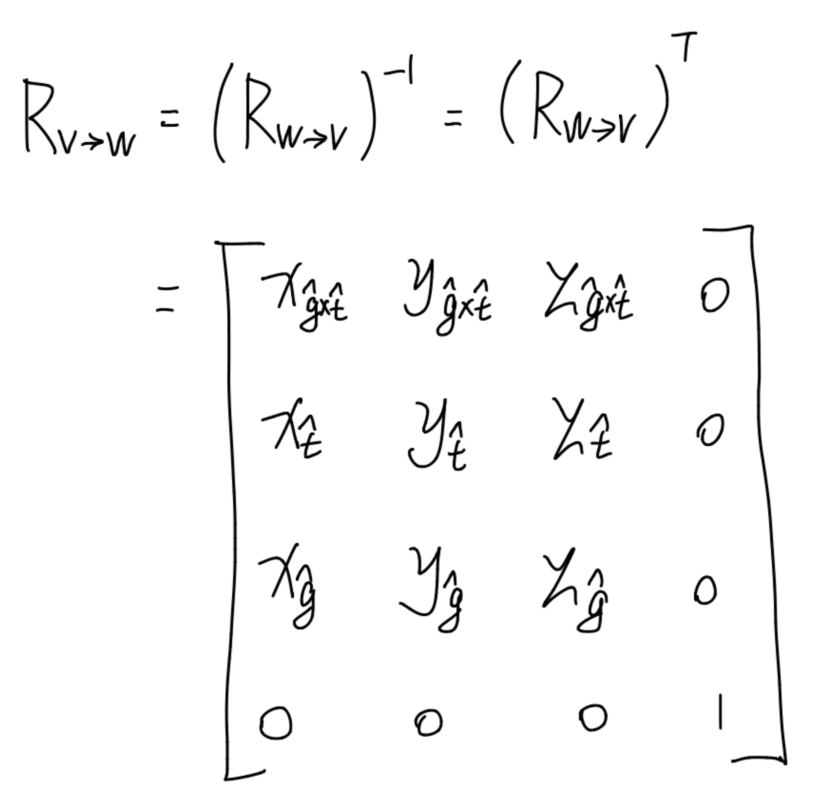
image-20211015000001680

总结一下就是

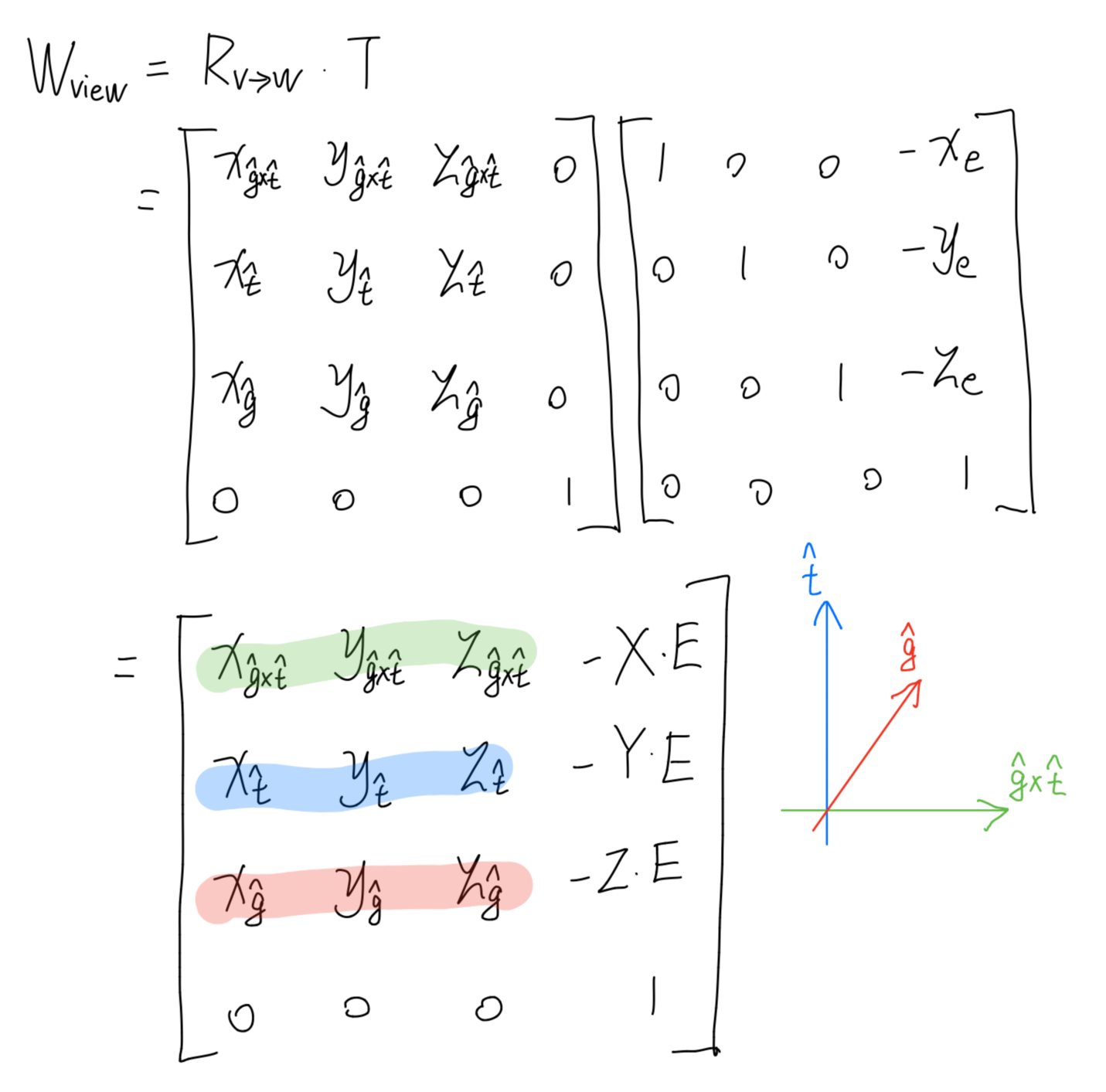
image-20211015002252091

裁剪空间

投影

所谓投影，其实是有2个操作

一是确定我们摄像机的可见空间，毕竟肯定不可能加载所有观察空间中的物体！

二是把可见空间（三维）中的物体投影到一个投影窗口（二维），投影窗口即类似于屏幕了（但不是屏幕空间）

首先我们定义可见视锥

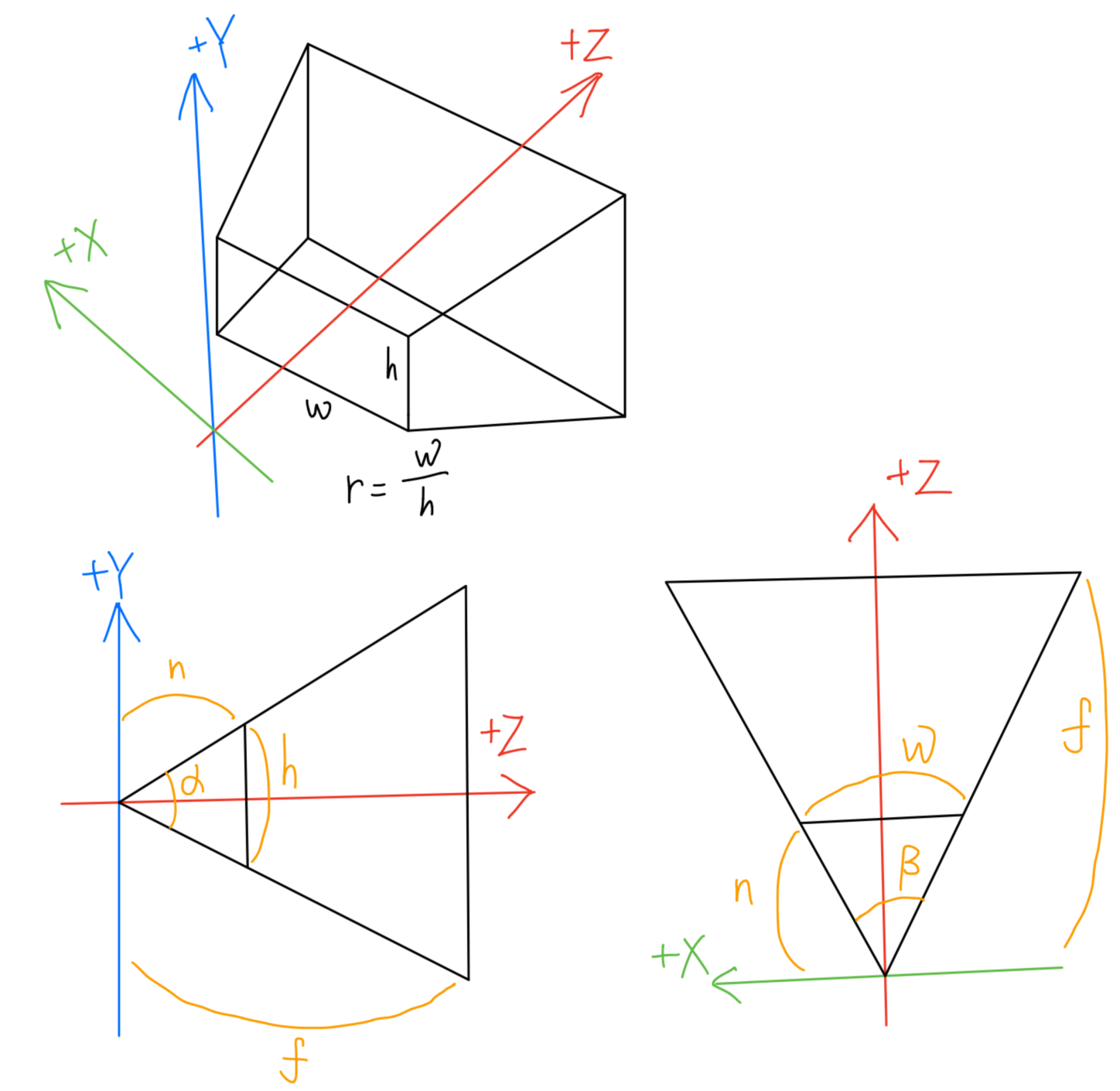
image-20211016023303730

首先轻松可以得到两个公式

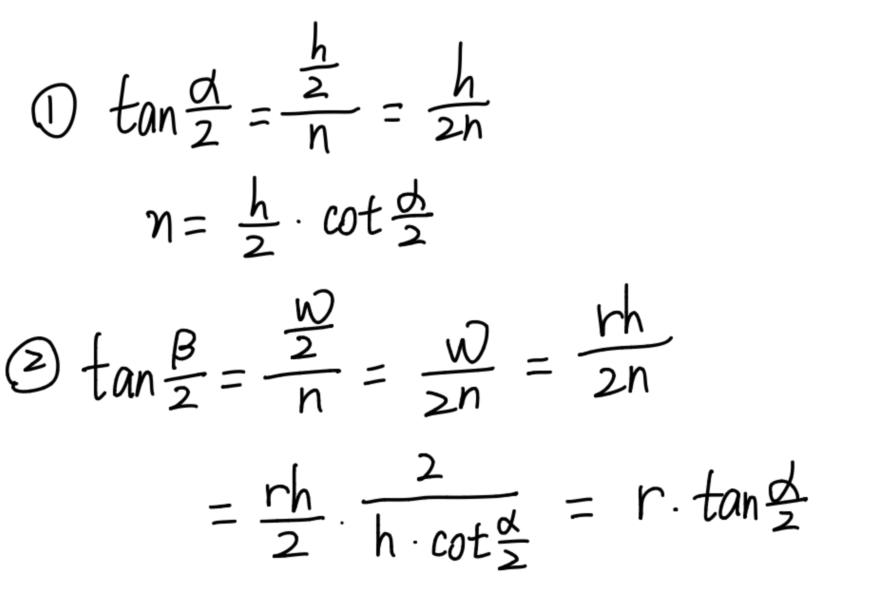
image-20211016032502062

目标是把视锥内的每一个点投影至近平面，利用相似三角形不难计算

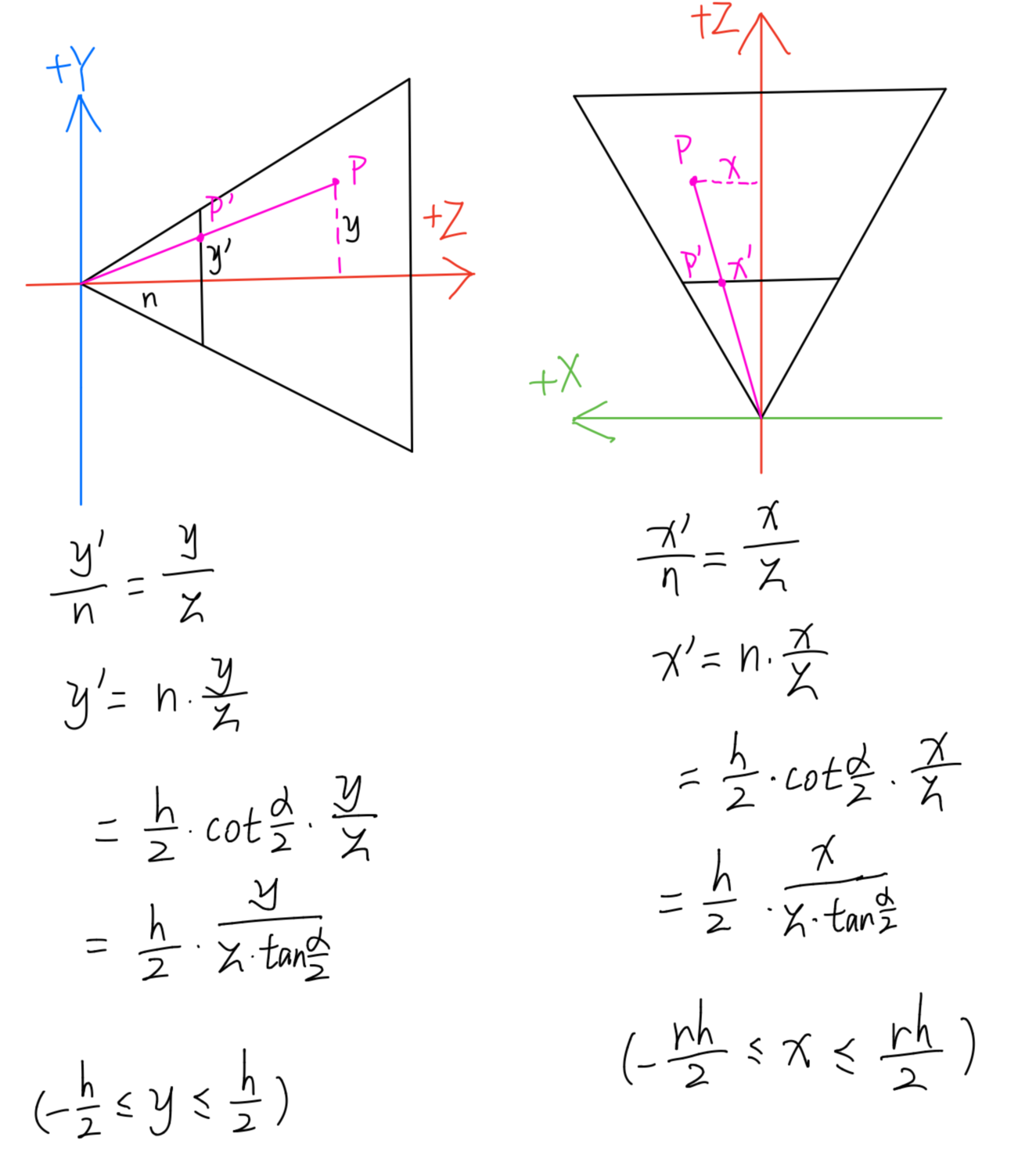
image-20211016033128795

NDC空间

经过上述计算后，x y的坐标仍然和h还有r有关系，而我们希望规格化坐标，使得x y均处于-1到1之间，则有

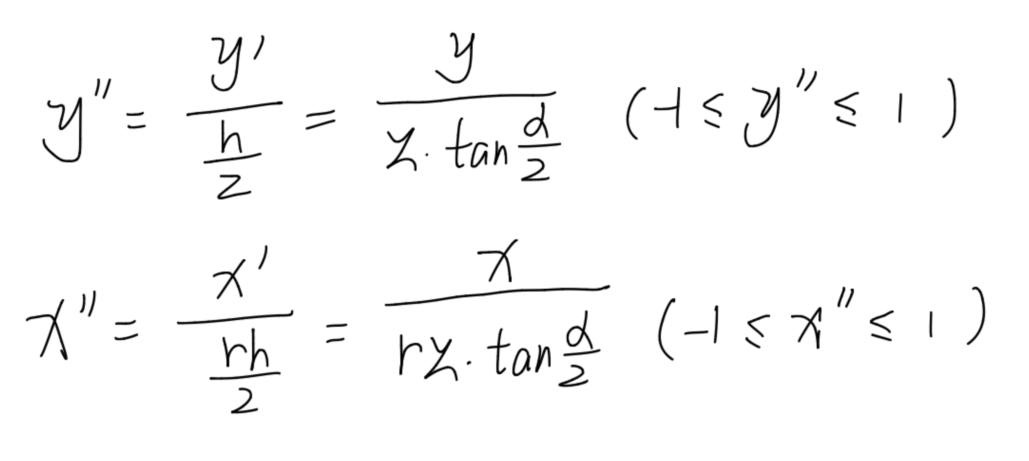
image-20211016041351015

矩阵

不难发现，y h r为定值，但z会随着x而变动，所以这不是一个线性变换，我们不能用一个矩阵直接来描述上述过程，那我们先用一个矩阵计算上述变换的线性部分，再对结果进行除Z，可以有以下推论

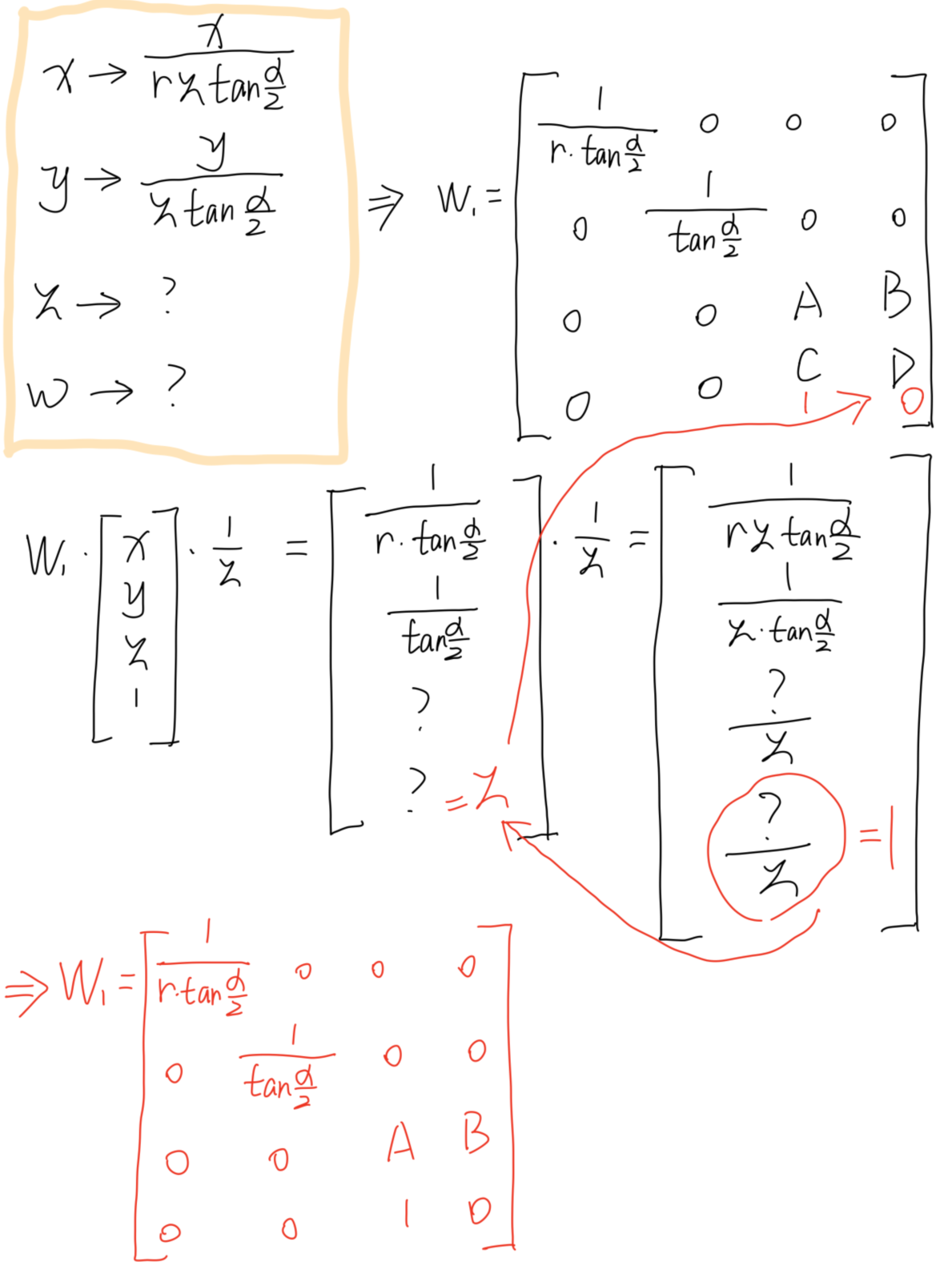
image-20211016042758142

最后

对于OpenGL，我们规定近裁面上的点最后会被投影到Z=-1，远裁面的点最后会被投影到Z=1

对于DIRECTX，我们规定近裁面上的点最后会被投影到Z=0，远裁面的点最后会被投影到Z=1

我们采用OpenGL的算法，假设现在有一个点X(x,y,z,1)

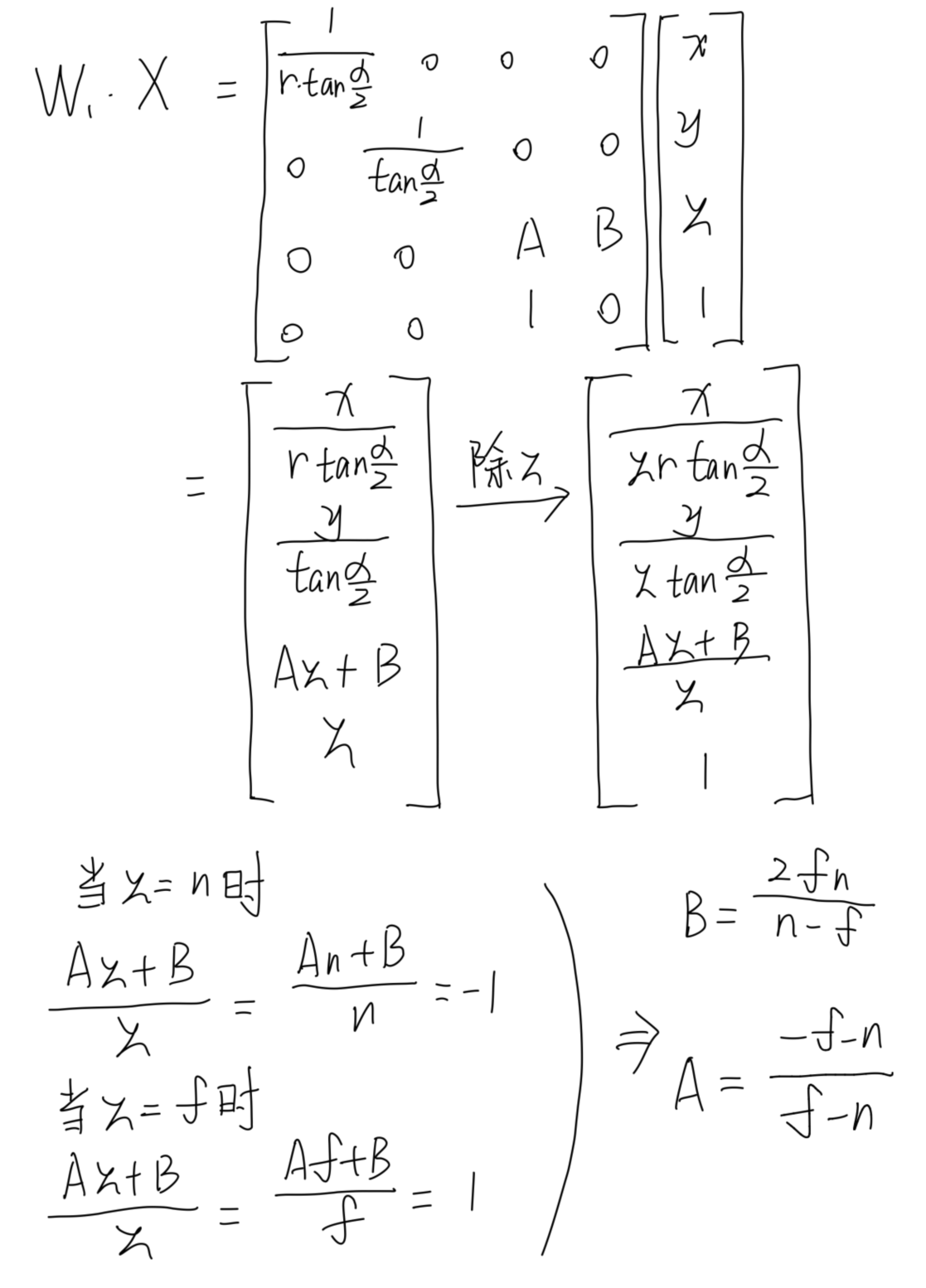
image-20211016043704660

W1为透视投影矩阵，在经过透视投影后，坐标处于齐次裁剪空间，此时需要进行一次除Z（透视除法），进入NDC空间

曲面细分阶段

略

几何着色阶段

会进行一次裁剪， 位于视锥外的顶点会被剔除，此操作发生在齐次裁剪空间，透视除法之前

光栅化阶段

视口变换

将NDC空间的坐标映射到屏幕，NDC空间中的X Y范围是-1至1，Unity屏幕左下角为原点，右上角为(w,h)，很容易得到转换公式

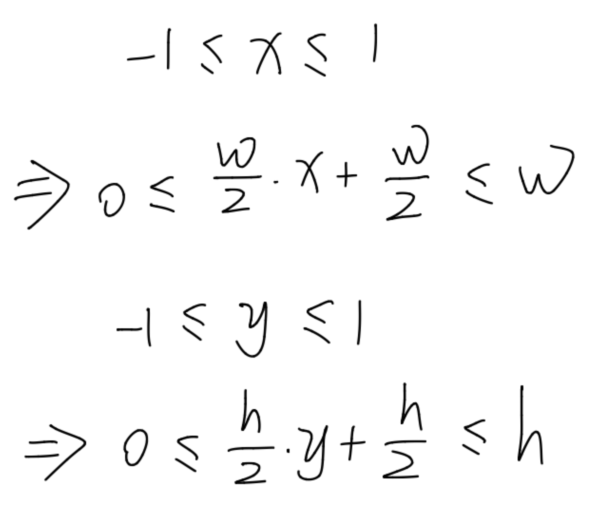
image-20211016044757408

背面剔除

略

顶点属性差值

三角形重心坐标公式

像素着色阶段

略

输出合并阶段

略